ANSWER
The man would have to invest $0.000000065 at an 87% interest rate to have $100000 after 35 years
To the nearest cent, it would be $0.00
Explanation:
Given information
The time for the investment = 35 years
The interest rate = 87%
The compounding period = 365
Total amount after the investment = $1,000, 000
Let the initial amount be P
To calculate the initial amount before the investment, we will need to apply the below formula
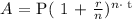
Where
A = final amount
P = initial amount
r = rate
t = time
n = compounding period
The next step is to convert 87% to decimal
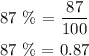
The next step is to substitute the given data into the compound interest formula

Therefore, the man would have to invest $0.000000065 at an 87% interest rate to have $100000 after 35 years