Question

Multiply each of the following and combine terms where possible: A. -a(a-b-8) B. (-6-a)(6+a) C. (a-b-2)(a+b+2)

Answer 1

A. -a² + ab + 8a

B. -36 - 12a - a²

C. a² - b² - 4b - 4

Step-by-step explanation:

To multiply each expression, we need to apply the distributive property. So, for each expression, we get

A.

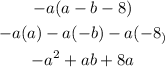
`\begin{gathered} -a(a-b-8) \\ -a(a)-a(-b)-a(-8_) \\ -a^2+ab+8a \end{gathered}`

B.

`\begin{gathered} (-6-a)(6+a) \\ -6(6)-6(a)-a(6)-a(a) \\ -36-6a-6a-a^2 \\ -36-12a-a^2 \end{gathered}`

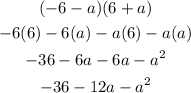
C.

`\begin{gathered} (a-b-2)(a+b+2) \\ a(a)+a(b)+a(2)-b(a)-b(b)-b(2)-2(a)-2(b)-2(2) \\ a^2+ab+2a-ab-b^2-2b-2a-2b-4 \\ a^2-b^2+(ab-ab)+(2a-2a)-2b-2b-4 \\ a^2-b^2-4b-4 \end{gathered}`

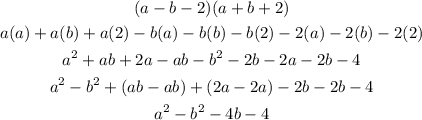
Therefore, the answers are

A. -a² + ab + 8a

B. -36 - 12a - a²

C. a² - b² - 4b - 4