Question

The radioactive isotope 14C has a half-life of approximately 5715 years. A piece of ancient charcoal contains only 42% as much of the radioactive carbon as a piece of modern charcoal. How long ago was the tree burned to make the ancient charcoal? (Round your answer to the nearest integer.)

Answer 1

The half life of carbon tells us how long it takes to get to half the original value. Thus, we can discover the decaying parameter of the exponential function, by doing the following:

`(C_0)/(2)=C_0e^(-\lambda *5715)\Rightarrow0.5=e^(-\lambda5715)\Rightarrow-5715\lambda=ln(0.5)`
`\lambda\approx1.2128*10^(-4)`

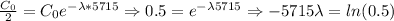
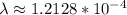
So, in order to find out how long it took to get to 42%, we can write is as the following:

`0.42C_0=C_0e^{-1.2128*10^(-4)t}\Rightarrow0.42=e^{-1.2128*10^(-4)t}`
`t=(ln(0.42))/(-1.2128*10^(-4))=7152.544\text{ years}`

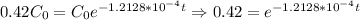
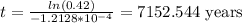
Thus, our answer is 7153 years