Question

What is the vertex of the graph of the function below?y = x2 - 4x + 3A. (1,-1)B. (2,0)C. (1,0)D. (2, -1)

Answer 1

The graph of a Quadratic function is a parabola.

You can see that the function has this form:

`y=ax^2+bx+c`

By definition, the x-coordinate of the vertex of a parabola can be found with this formula:

`h=-(b)/(2a)`

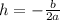
Where "h" is the x-coordinate of the vertex of the parabola.

Given this function:

`y=x^2-4x+3`

You can identify that:

`\begin{gathered} a=1 \\ b=-4 \\ c=3 \end{gathered}`

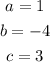
Then, you can substitute values into the formula, in order to find the x-coordinate of the vertex of the parabola. This is:

`h=-((-4))/(2(1))=2`

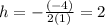
Knowing this value, you can substitute it into the Quadratic equation and then you must evaluate, in order to find the y-coordinate of the vertex of the parabola. This is:

`\begin{gathered} y=(2)^2-4(2)+3 \\ y=4-8+3 \\ y=-1 \end{gathered}`

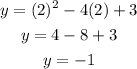
So the vertex of the parabola is:

`(2,-1)`

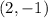
The answer is: Option D.