Question

Helene invested a total of $1,000 in two simple-interest bank accounts. One account paid 5% annual interest; the other paid 8% annual interest. The total amount of interest she earned after 1 year was $65. Find the amount invested in each account.

Answer 1

Explanation:

Let
`\textbf{\textit{x}}` be the amount invested into the account with a 5% annual interest and
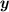`\textit{\textbf{y}}` be the amount invested into the account with an 8% annual interest,

It is stated that Helene invested a total of $1000, which can be written mathematically as

`x \ + \ y \ = \ 1000 \ \ \ \text{----- \ (1)}` .

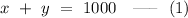Subsequently, the total amount of interest after 1 year is $65. This statement can be changed into the equation below.

`0.05x \ + \ 0.08y \ = \ 65 \ \ \text{----- \ (2)}` .

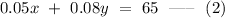First, divide each term in equation (2) by 0.05, yields the expression

`x \ + \ 1.6y \ = \ 1300 \ \ \text{----- \ (3)}` .

Then, let equation (1) be subtracted from equation (3) term-by-term,

`(x \ + \ 1.6y ) \ - \ (x \ + \ y) \ = \ 1300 \ - \ 1000 \\ \\ (x \ - \ x) \ + \ (1.6y \ - \ y) \ = \ 300 \\ \\ \-\hspace{3.15cm} 0.6y \ = \ 300 \\ \\ \-\hspace{3.38cm} \displaystyle(3)/(5)y \ = \ 300 \\ \\ \-\hspace{3.65cm} y \ = \ 500`.

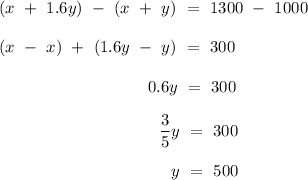Therefore, the amount invested in each account is $500.

Answer 2

a = total amount invested at 5%

b = total amount invested at 8%

we know 5% was earned in interest from "a", so that'd be (5/100) * a or 0.05a.

we know 8% was earned in interest from "b", so that'd be (8/100) * a or 0.08b.

we also know that the total for both is 1000, a + b = 100.

`\begin{cases} a + b = 1000\\ 0.05a+0.08b=65 \end{cases}\qquad \qquad \stackrel{\textit{since we know}}{a+b=1000}\implies b = 1000-a \\\\\\ \stackrel{\textit{substituting on the 2nd equation}}{0.05a+0.08(100-a)=65}\implies 0.05a+80-0.08a=65 \\\\\\ -0.03a+80=65\implies -0.03a=-15\implies a=\cfrac{-15}{-0.03}\implies \boxed{a = 500} \\\\\\ \stackrel{\textit{we know that}}{b = 1000-a}\implies b=1000-500\implies \boxed{b = 500}`