Question

The mean of the data for the resting heart rate of adults is 71 beats perminute, and the standard deviation is 3 beats per minute. The results of the data were normally distributed.About what percentage of the population has a resting heart ratebetween 71 and 74?

Answer 1

Given:

Mean = 71 beats per minute

Standard deviation = 3 beats per minute

Required:

The percentage of the population that has a resting heart rate between 71 and 74

First, we convert to data to z-score values using the relationship below:

`\begin{gathered} z\text{ = }\frac{x\text{ - }\mu}{\sigma} \\ \text{where }\mu\text{ is the mean} \\ \sigma\text{ is the standard deviation} \end{gathered}`

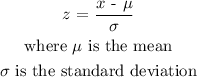
Z-score for 71 beats per minute:

`\begin{gathered} z_1\text{ = }\frac{71\text{ - 71}}{3} \\ =\text{ 0} \end{gathered}`

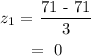
Z-score for 74 beats for minute:

`\begin{gathered} z_2\text{ = }\frac{74\text{ - 71}}{3} \\ =\text{ 1} \end{gathered}`

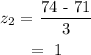
Using the normal distribution table, we can find the probability of having a population with a z-score between 0 and 1.

So,

`\begin{gathered} P(0\text{ }\leq\text{ x }\leq\text{ 1) = 0.84134 - 0.5} \\ =\text{ 0.34134} \end{gathered}`

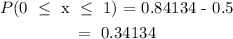
The percentage of the population that has a resting heart rate between 71 and 74 is :

`\begin{gathered} =\text{ 0.34134 }*\text{ 100\%} \\ =\text{ 34\% (nearest percent)} \end{gathered}`

Answer = 34%