Question

Hello help me with this question thanks in advance​

Answer 1

1:c

2:a

3:d

4:b

5:d

Explanation:

In rhombus STAR

`1.SAL\ \ TR`
`\left\{Characteristic\ of\ rhombus\right\}`

`SO < SKR=90`°

`2. < RAK=(1)/(2) < RAT=32`°

`3. < ARS+ < RAT=180`°

`< ARS=180`°
`- < RAT`

`=116`°

`4.\ < KRS=(1)/(2) < ARS`

`=58`°

`5.\ < SKR= < AKR= < SKT`

`= < AKT=90`°

I hope this helps you

:)

Answer 2

`\bold{\huge{\pink{\underline{ Solution }}}}`

Solution 1 :-

The measure of Angle SKR is 90°

• In Rhombus, The diagonals bisect each other at 90° it means diagonals are perpendicular to each other.

Hence, Option C is correct

Solution 2 :-

The measure of Angle RAK is 32°

• We have given that angle RAT is 64° but here AK is acting as a bisector of Angle RAT

Therefore,

`\sf{\angle{RAT = 2 }} {\sf{\angle{RAK}}}`

`\sf{( 64)/(2)}{\sf{=}}{\sf{\angle{RAK}}}`

`\sf{\angle{ RAK = 32°}}`

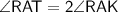
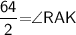
Hence, Option a is correct

Solution 3 :-

The measure of Angle ARS is 116°

• Opposite angles of rhombus are equal

`\sf{\angle{ARS = }}{\sf{\angle{ATS}}}`

So,

`\sf{\angle{RSK = }}{\sf{\angle{RAK}}}`

`\sf{\angle{ RSK = 32° }}`

By using Angle sum property

AngleRSA + AngleSAR + AngleARS = 180°

`\sf{ 32° + 32° + }{\sf{\angle ARS = 180° }}`

`\sf{\angle {ARS = 180° - 64° }}`

`\sf{\angle{ARS = 116° }}`

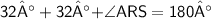
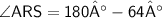
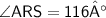
Hence, Option d is correct

Solution 4 :-

The measure of angle KRS is 58°

• We know that angle ARS is 116° but here RK is acting as a bisector of Angle ARS

Therefore ,

`\sf{\angle{ARS}}{\sf{ = 2}}{\sf{\angle KRS}}`

`\sf{( 116)/(2)}{\sf{=}}{\sf{\angle{KRS}}}`

`\sf{\angle{ KRS = 58°}}`

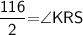
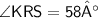
Hence, Option b is correct

Solution 5 :-

mAngleSKR = All of the above

• In rhombus, the diagonals bisect each other at 90°

From Above, we can say that,

mAngleSKR + mAngleAKR + mAngleAKT + mAngleSKT = 90°

Hence, Option D is correct.