To find the zeros in a function you have to find those values that make that:
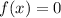
In this case you have an cubic equation so first we are going to factorize it:
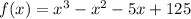
Knowing that 125 is equal to:
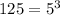
this function can be expressed like:
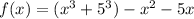
The sum of cubes is:
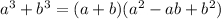
We can use this to the first part of the equation:
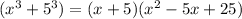
Now we can factorize the other part as follow:
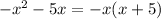
So the equation now is:
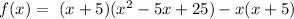
Now we can factorize the (x+5) as a common term

And if we organice this one we get:
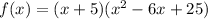 using he first part ( x + 5) we can find one zero, as follow:
using he first part ( x + 5) we can find one zero, as follow: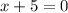

Finally we can use the quadratic equation in the second part we can find the other zeros, as follow:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
![x=\frac{-(-6)\pm\sqrt[]{(-6)^2-4(1)(25)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/6jflh3dj1gbev1k1qxc5pnm9i2f5u1107a.png)
![x=\frac{6\pm\sqrt[]{36-100}}{2}=\frac{6\pm\sqrt[]{-64}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/6311napo6nat57l5erzkc2fxtqghtmiysc.png)
As we get a root for a negative munber we can use the imaginary number:
![\sqrt[]{-64}=8i](https://img.qammunity.org/2023/formulas/mathematics/college/x8ipy6vsz7kc6drol6dfl31vs95qg9976z.png)
So:
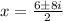
The zeros are now calculated with the two solutions ( + and -)

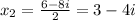
Then so, the zeros of the function
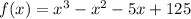
are:
- 5
3 + 4i
3 - 4i
option B