Hello there. To solve this question, we'll have to remember some properties about exponentiation.
We have the following expression:
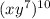
First, remember the power product rule:
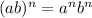
And the power of a power rule:
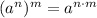
In this case, we have:
Applying the power product rule
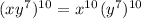
Now, apply the power of a power rule
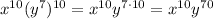
This is the simplified form of this expression.