Let x and y represent the cost of one box of popcorn and one soft drink respectively.
Given;
Ms. Torres purchased two boxes of popcorn and three soft drinks for $6.05.
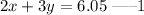
Also, Mr. Russo purchased three boxes of popcorn and five soft drinks for $9.50.
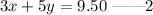
From the question we have generated a system of simultaneos equation.
we now need to solve the simultaneous equation to get the value of x and y.
Let's solve by elimination.
Firstly multiply equation 1 through by 3 and equation 2 by 2.
This is to have equal coefficient of x for the two equations, to make elimination possible.
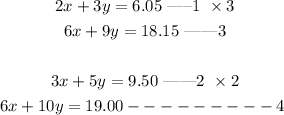
Now we have equation 3 and 4.
Let us subtract equation 3 from 4.
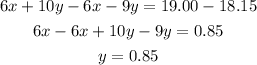
We can now substitute the value of y into equation1 to get x