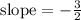Step 1. The two points that we have are:

And we are required to find the slope of the line that passes through these points.
Step 2. We will label the two points as (x1,y1) and (x2,y2):
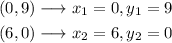
Step 3. To find the slope, we will use the slope formula:
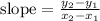
Substituting the known values:
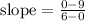
Step 4. Simplify the operations:

Step 5. Simplify the fraction.
Both numbers 9 and 6 can be divided by 3.
9 divided by 3 is equal to 3,
and 6 divided by 3 is equal to 2.
Therefore, the fraction can be simplified as follows:
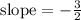
Answer: