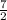Solution:
The equation of a circle is expressed as
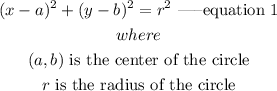
Expanding equation 1 gives:
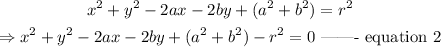
Given the equation of the circle to be expressed as
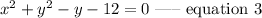
Comparing equations 2 and 3, we have
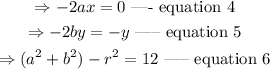
From equation 4,

From equation 5,

From equation 6,
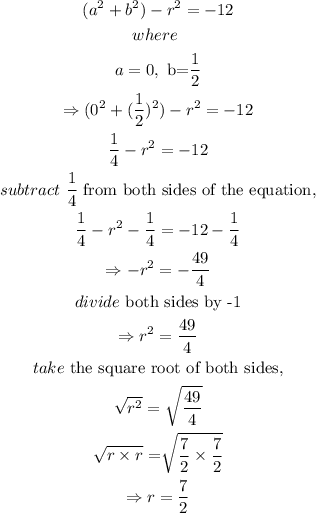
Hence, the radius of the circle is