Question

1. (06.07 HC) An expression is shown below: 4(m + 3 + 5m) Part A: Write two expressions that are equivalent to the given expression. (3 points) Part B: Show that one of your expressions in Part A is equivalent to the given expression using algebraic properties. Explain which properties you used Part C: Show that your other expression from Part A is equivalent to the given expression by substituting a number for m. (3 points) B i U Font Family AA AOS - 4(m + 5 + 3m) 3(m + 4 + 5m) part a parib partc

Answer 1

The given expression is

`4(m+3+5m)`

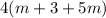
Part A.

We get the first equivalent expression by combining the like terms

`4(6m+3)`

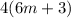
We get the second equivalent expression by using the distributive property

`24m+12`

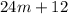
Part B.

To show the equivalence between the given expression and one of the part A expressions, we just have to extract the greatest common factor of 24m + 12, which is 4.

`4(6m+3)`

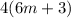
Then, we separate the term 6m into m+5m

`4(m+5m+3)`

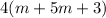
At last, we use the commutative property

`4(m+3+5m)`

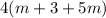
There you have it, the equivalence has been demonstrated.

Part C.

Let's evaluate the expressions when m = 1.

`4(m+3+5m)=4(1+3+5\cdot1)=4(1+3+5)=4(9)=36`
`24m+12=24\cdot1+12=24+12=36`

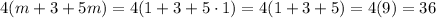
As you can see, using m = 1, we proved that the expressions were equivalent.