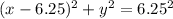Answer:
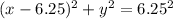
Explanation:
Given the equations of the lines that represent the sides of the triangle, the diagram on the coordinate plane;
Given the lines and the three vertices of the triangle. Let P(a,b) be the center of the circle.
Therefore,
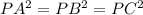
If A(12.5,0), B(8,6) and C(0,0)

Solve for ''a'' and ''b'':
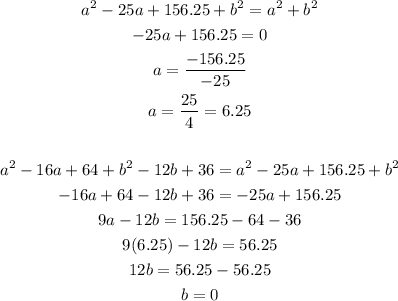
Then, the radius of the circle is:
![\begin{gathered} PA=\sqrt[2]{(a-12.5)^2+b^2} \\ PA=6.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cltd2of61tswvv0xcabavafqwq19hscilc.png)
Hence, the equation of the circle is given as: