Question

use formulas to find the lateral area and surface area of the prism .The lateral area of the prism is _ in2(Round to the nearest whole number as needed .)

Answer 1

Answer: Lateral area = 750 square inches

Lateral area of a prism is given as

`Lateral\text{ area = Perimeter of the prism + height of the prism}`

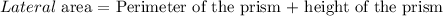
Perimeter = a + b + c

Firstly, we need to find the base using pythagoras theorem

`\begin{gathered} \text{Hypotenus}^2=opposite^2+adjacent^2 \\ \text{Let the base = x} \\ 17^2=15^2+x^2 \\ 289=225+x^2 \\ \text{Isolate x}^2 \\ x^2\text{ = 289 - 225} \\ x^2\text{ = 64} \\ \text{Take the square root of both sides} \\ \text{x = }\sqrt[]{64} \\ x\text{ = 8 in} \end{gathered}`

Lateral area = Perimeter x height

Perimeter = a + b + c

Perimeter = 17 + 17 + 16

Perimeter = 50 inches

Lateral area = 50 x 15

Lateral area = 750 square inches

Therefore, the lateral area of the prism is 750 square inches