1 Answer

John Offenhartz · Answer 1 · 2023-11-07T03:10:26+0000

10)

In general, the sum of the inner angles of a polygon is given by the formula below

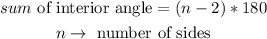
$\begin{gathered} sum\text{ of interior angle}=(n-2)*180\degree \\ n\rightarrow\text{ number of sides} \end{gathered}$

Therefore, in our case, since we are dealing with a polygon of seven sides,

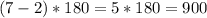
$\begin{gathered} (7-2)*180\degree=5*180\degree=900\degree \\ \end{gathered}$

Then,

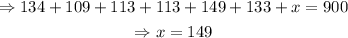
$\begin{gathered} \Rightarrow134+109+113+113+149+133+x=900 \\ \Rightarrow x=149 \end{gathered}$

Thus, the answer to question 10 is x=149°.

11)

Using the formula for the sum of the inner angles of a polygon used in part 10),

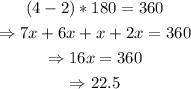
$\begin{gathered} (4-2)*180=360 \\ \Rightarrow7x+6x+x+2x=360 \\ \Rightarrow16x=360 \\ \Rightarrow22.5 \end{gathered}$