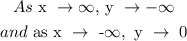Question

Graph each exponential function. Identify a, b, the y-intercept, and the end behavior of the graph. F(x)= -3(3)^x

Answer 1

Step 1 :

In this question, we are meant to graph the exponential function,

`\text{f ( x ) = -3 ( 3 )}^x`

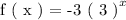
Step 2 :

when x = -2, we have that:

`\begin{gathered} f(x)=-3(3)^x \\ f(-2)=-3(3)^(-2) \\ f(-2)=\text{ - 3 x }(1)/(3^2)\text{ = }(-3)/(9)\text{ } \\ f\text{ (- 2 ) =}(-1)/(3) \end{gathered}`

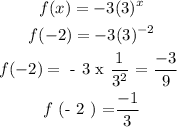
when x = -1, we have that :

`\begin{gathered} f(-1)=-3(3)^(-1)^{} \\ f(-1)=\text{ -3 x }(-1)/(3) \\ f(-1)=\text{ 1} \end{gathered}`

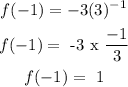
when x = 0, we have that:

`\begin{gathered} f(0)=-3(3)^0 \\ f(0)=\text{ -3 x 1} \\ f\text{ ( 0 ) = -3} \end{gathered}`

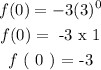
when x = 1 , we have that:

`\begin{gathered} f(1)=-3(3)^1 \\ f(1)=\text{ - 3 x 3 } \\ f\text{ ( 1 ) = -9} \end{gathered}`

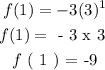
when x = 2 , we have that:

`\begin{gathered} f(2)=-3(3)^2 \\ f\text{ ( 2) = -3 x 9} \\ f\text{ ( 2) = -27} \end{gathered}`

Step 3 :

Since the function is in the form of

`f(x)=a(b)^x`

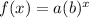
comparing with the function,

`f(x)=-3(3)^x`

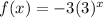
We have that:

a = -3

b = 3

y -intercept ( where the value of x = 0 ) :

y = -3

Step 4 :

End behavior:

`\begin{gathered} As\text{ x }\rightarrow\infty\text{, y }\rightarrow-\infty \\ and\text{ as x }\rightarrow\text{ -}\infty,\text{ y }\rightarrow\text{ 0} \end{gathered}`