Let A₀ be the initial mass of the sample of the radioactive substance.
Since half of the substance decays each day, then, the next day the amount of radioactive substance left is:
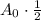
After t days, the total amount would have decayed by 1/2, t times. Then, the amount A of the radioactive substance left after t days is:
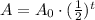
To find how many grams of the substance would be left after one week, replace A₀=100 and t=7:

Therefore, the exponential model that tells the amount of substance remaining on a given day, is:
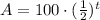
And the amount of grams left after a week is 0.78.