Question

Consider the functions f(x) = (x - 5)2 + 2 and g (x) = (x + 6)2 - 4. Which of the followstatements is true?The graph of g (x) is shifted 2 units below and one unit to the right to the graph of f(x).The graph of g (x) is shifted one unit above and 2 units to the right of the graph of f(x).The graph of g (x) is shifted 6 units below and 11 units to the left to the graph of f(x).The graph of g(x) is shifted 11 units above and 6 units to the left to the graph of f(x).The graph of g (x) is shifted 11 units above and 6 units to the left to the graph of f(x).

Answer 1

Given:

`f(x)=(x-5)^2+2`
`g(x)=(x+6)^2-4`

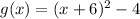
Required:

We need to find the transformation.

Step-by-step explanation:

Consider the function.

`g(x)=(x+6)^2-4`

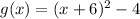
Replace x =x-11 in the function.

`g(x-11)=(x-11+6)^2-4`

`g(x-11)=(x-5)^2-4`

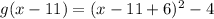
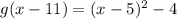
Add 6 to both sides of the equation.

`g(x-11)+6=(x-5)^2-4+6`

`g(x-11)+6=(x-5)^2+2`

`Substitute\text{ }f(x)=(x-5)^2+2\text{ in the equation.}`

`g(x-11)+6=f(x)`

`f(x)=g\mleft(x-11\mright)+6`

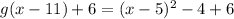
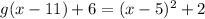
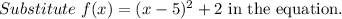
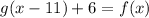
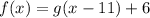
We know that if f(x)=g(x-k)+h the g(x) shifts k units left and h and shifts h units above.

Here the graph of g (x) is shifted 11 units above and 6 units to the left to the graph of f(x).

Final answer:

The graph of g (x) is shifted 11 units above and 6 units to the left to the graph of f(x).