ANSWER
Step-by-step explanation
The distance between two points a dna b on a number line is given as:
|a - b|
Given that point a is greater than point b.
To locate the midpoint between point a and point b, we can use the formula for distance given above.
Because the midpoint is the point that divides a distance (between two points) into two equal halves, then we have to simply find half of the distance.
Because we have to consider possible positive and negative values of a and b, the absolute value cannot play a role in the formula.
This is because absolute value is always positive and that is not always the case for the midpoint of a and b.
Therefore, the midpoint between a and b is:
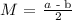
This formula works for both positive and negative values of a and b.
In the real world, we can use the formula to find the midpoint between two positions on a map.