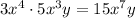The expression we have is:
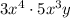
To simplify this expression, we will use the following property of exponents:
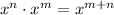
We add the exponents when we multiply variables.
But first, we have to multiply the coefficients, since 3*5 is equal to 15, we have:
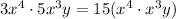
And now we do apply the rule we mentioned for multiplying variables.
We add the exponents 4 and 3 of the x:
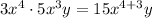
Since 4+3 is equal to 7, we have the final answer: