Question

The length of a rectangle is 2 inches more than the width. The area is 24 square inches. Find the dimensions.The length of the rectangle is ? inches, while the width is ? inches.

Answer 1

In general, the area of a rectangle is given by the formula below

`A=lw`

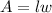
where l is its length and w its width.

Furthermore,

`\begin{gathered} l=w+2 \\ \text{and} \\ lw=24 \end{gathered}`

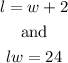
Solving the system of equations,

`\begin{gathered} l=w+2 \\ \Rightarrow(w+2)w=24 \\ \Rightarrow w^2+2w-24=0 \end{gathered}`

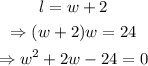
Use the quadratic formula to find w, as shown below,

`\begin{gathered} w^2+2w-24=0 \\ \Rightarrow w=\frac{-2\pm\sqrt[]{4-4\cdot-24}}{2}=\frac{-2\pm\sqrt[]{4-4\cdot-24}}{2}=\frac{-2\pm\sqrt[]{100}}{2} \\ \Rightarrow w=-1-5,-1+5 \\ \Rightarrow w=-6,4 \end{gathered}`

Since w is a length, it cannot be negative; therefore, w=4

Finding l,

`\begin{gathered} w=4 \\ \Rightarrow l=4+2=6 \\ \Rightarrow l=6 \end{gathered}`

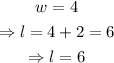
The length is 6in and the width is 4in.