Answer:
The axis of symmetry = -1
The vertex = (-1, 1/2)
The domain = all real numbers
The range = all real numbers less than or equal to 1/2
Explanations:
The given function is:
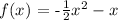
Note that for a function, f(x) = ax² + bx + c, the axis of symmetry is given by:
x = -b/2a
From the given function f(x):
a = -1/2, b = -1, c = 0
The axis of symmetry is therefore calculated as:
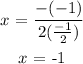
Axis of symmetry: x = -1
The vertex of a quadratic equation is given as (h, k)
The axis of symmetry is the x-coordinate of the vertex, therefore, h = -1
To find k, let x = h and f(x) = k in the given equation
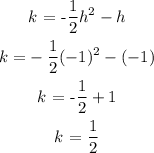
The vertex of the equation = (-1, 1/2)
Since f(x) is a quadratic function, the domain of the function f(x) is a set of all real numbers
To find the range:
Since a = -1/2 < 0, the graph is opening downwards.
Therefore, the range is given as y ≤ k
Since k = 1/2, the range is y ≤ 1/2