Question

Mandy and her friend Lucy are knitting scarves for the homeless. Mandy had already completed 10 scarves and has committed to making 1 more scarf per day Lucy, who hasn't completed any scarves yet has more free time and can make 2 scarves per day. At some point, Lucy will catch up and they will both have completed the same number of scarves. How long will that take? Write a system of equations, graph them and type the solution.

Answer 1

We will find the time it will take Lucy to catch up to Mandy, by solving the following system:

`\begin{cases}y=d+10 \\ y=2d\end{cases}`

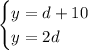
Here, the first expression represents Mandy's and the second expression represents Lucy's.

Now, we solve:

`2d=d+10\Rightarrow d=10`

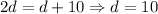
From this, we have that it will take 10 days to have the same number of scarves, which will be 20 scarves.

We can graph them as follows: