To find r, we have to use the law of cosines because the triangle is not right.
![\begin{gathered} r^2=9^2+7.5^2-2(9)(7.5)\cos 89 \\ r=\sqrt[]{81+56.25-2.36} \\ r\approx11.6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ub9mlzju8v2hbdhofhjllpkk6pacihunzh.png)
Then, we find the angles using the law of sines.
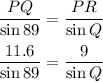
Let's solve for Q.
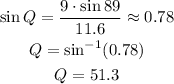
At last, we find the angle P using the interior angles theorem
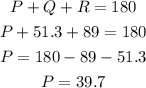
Hence, r = 11.6, angle Q is 51.3°, and angle P is 39.7°.