Answer:
-(√3 + 1)/2
Step-by-step explanation:
We will use the following properties:
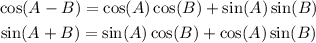
First, let's calculate cos(150). Since 150 = 180 - 30, we get:
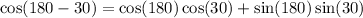
Taking into account that cos(180) = -1 and sin(180) = 0, we get:
![\begin{gathered} \cos (150)=-1\cdot\frac{\sqrt[]{3}}{2}+0\cdot(1)/(2) \\ \cos (150)=-\frac{\sqrt[]{3}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rfyehcxcsoac241skce9jambk75gxlezke.png)
On the other hand, 210 = 180 + 30, so sin(210) will be equal to:
![\begin{gathered} \sin (180+30)=\sin (180)\cos (30)+\cos (180)\sin (30) \\ \sin (210)=0\cdot\frac{\sqrt[]{3}}{2}+(-1)\cdot(1)/(2) \\ \sin (210)=-(1)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ceqb7e2gnj1i5lecjiaxkp849xti6dkpwy.png)
Therefore, cos (150) + sin(210) is equal to:
![\cos (150)+\sin (210)=-\frac{\sqrt[]{3}}{2}-(1)/(2)=-\frac{(\sqrt[]{3}+1)}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/j9w3panvh6ea0jx7wqy0ymiroo3w967rrv.png)
So, the answer is: -(√3 + 1)/2