Question

Customers of a phone company can choose between two service plans for lng distance calls. The first plan has an $11 monthly fee and charges an additional $0.12 for each minute of calls. The second plan has a $15 monthly fee and charges an additional $0.08 for each minute of calls. For how many minutes of calls will the costs of the two plans be equal?

Answer 1

Let y be the total cost for x minutes of phone calls.

The slope-intercept form of a linear relation between x and y is:

`y=mx+b`

Where m is the slope of the line and represents the rate of change of y with respect to x, and b is the y-intercept of the line and represents the initial value.

The first plan has a rate of change of $0.12 for each minute, and an initial value (which is the fee when 0 minutes of calls are used) of $11. Then, the equation that describes this plan is:

`y=0.12x+11`

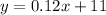
The second plan has an initial value of $15 and a rate of change of $0.08. The equation for this one, is:

`y=0.08x+15`

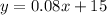
If x is such that both plans have the same cost, then:

`\begin{gathered} 0.12x+11=0.08x+15 \\ \Rightarrow0.12x-0.08x=15-11 \\ \Rightarrow0.04x=4 \\ \Rightarrow x=(4)/(0.04) \\ \Rightarrow x=100 \end{gathered}`

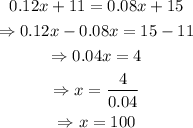
Therefore, the two plans have the same cost when the number of minutes of calls is equal to 100.