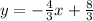Question

Write an equation of the line that passes through the given point and is parallel to the given line. Your answer should be written in slope-intercept form.P(5, -4), x = −3/4y + 6

Answer 1

Step-by-step explanation:

Given;

We are given the following equation;

`x=-(3)/(4)y+6`

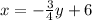
Required;

We are required to write the equation of a line that is parallel to the one given and which passes through the point

`P(5,-4)`

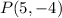
Step-by-step solution;

We shall begin by re-writing the equation given in slope-intercept form;

`\begin{gathered} Slope-intercept\text{ }form: \\ y=mx+b \end{gathered}`

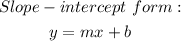
We shall now take the equation and make y the subject, as shown below;

`\begin{gathered} x=-(3)/(4)y+6 \\ Add\text{ }(3)/(4)y\text{ }to\text{ }both\text{ }sides: \\ x+(3)/(4)y=-(3)/(4)y+(3)/(4)y+6 \\ Subtract\text{ }x\text{ }from\text{ }both\text{ }sides: \\ x-x+(3)/(4)y=-(3)/(4)y+(3)/(4)y-x+6 \end{gathered}`

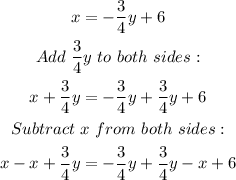
We can now simplify the above;

`(3)/(4)y=-x+6`

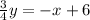
To cancel the coefficient of y, multiply both sides by 4/3. We now have the following;

`(4)/(3)*(3y)/(4)=(4)/(3)*(-x+6)`
`\begin{gathered} y=(4(-x+6))/(3) \\ \\ y=(-4x+24)/(3) \\ \\ y=-(4x)/(3)+(24)/(3) \\ \\ y=-(4x)/(3)+8 \end{gathered}`

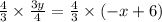
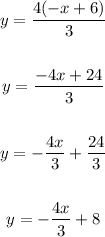
Now we have the slope of the line as

`m=-(4)/(3)`

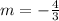
Please remember the slope is the coefficient of x.

Also, take note that for two lines that are parallel to each other, the slopes are the same.

This means the slope of the equation we are required to find is also -4/3.

We now have the following;

`\begin{gathered} (x,y)=(5,-4) \\ m=-(4)/(3) \end{gathered}`

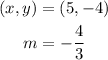
We shall now substitute the values into the equation in slope-intercept form;

`\begin{gathered} y=mx+b \\ \Rightarrow-4=-(4)/(3)(5)+b \\ \\ -4=-(20)/(3)+b \end{gathered}`

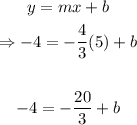
Add 20/3 to both sides;

`\begin{gathered} (20)/(3)-4=b \\ \\ Take\text{ }the\text{ }LCM\text{ }for\text{ }the\text{ }left\text{ }side\text{ }of\text{ }the\text{ }equation: \\ (20)/(3)-(12)/(3)=b \\ \\ (8)/(3)=b \end{gathered}`

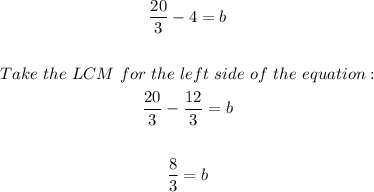
Now we have the values of m and b, the equation will be as shown below;

`\begin{gathered} y=mx+b: \\ y=-(4)/(3)x+(8)/(3) \end{gathered}`

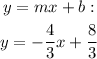
ANSWER:

`y=-(4)/(3)x+(8)/(3)`