Answer:
The mass of urea that can be manufactured is 5,000,832.65g.
Step-by-step explanation:
1st) It is necessary to balance the chemical reaction:
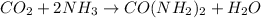
From the balanced reaction we know that from 1 mole of CO2, we obtain 1 mole of urea.
2nd) We have to calculate the amount of CO2 that we have, if there are 1.00x10^3 kg (1,000,000 g) of carbon:
- CO2 molar mass: 44.01g/mol
- C atomic mass: 12.01g/mol
In 44.01g of CO2, there are 12.01g of carbon (C). With a mathematical rule of three we can calculate the amount of CO2:
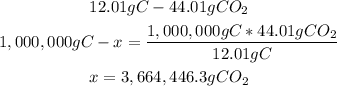
There are 3,664,446.3g of CO2 from 1,000,000g of C.
3rd) From the stoichiometry of the reaction, we know that from 44.01g (1 mole) of CO2, we can obtain 1 mole of urea (urea molar mass: 60.06g/mol). With a mathematical rule of three we can calculate the mass of urea that can be manufactured from 3,664,446.3g of CO2:
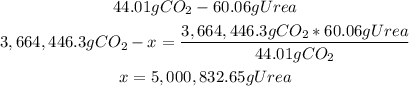
So, the mass of urea that can be manufactured is 5,000,832.65g.