Explanation:
Notes:
Headwind opposes forward motion, meaning that the plane moves slower.
Tailwind boosts forward motion, meaning that the plane moves faster.
Given:
The jet can fly 837 miles against a 15-mph headwind.
The jet can fly 1023 miles with a 15-mph Tailwind, given the same amount of time for the headwind.
Solve:
We're trying to find the speed of the jet when there's no wind boosting or counteracting the speed.
The speed has to be in-between 837 and 1023.
Let's find the number in-between 837 and 1023.
Subtract:

Divide 186 by 2:
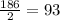
Add 93 to 837:
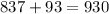
The plane's speed is 930 miles without no wind, in the given time.