ANSWER
![0.01\operatorname{cm}]()
Step-by-step explanation
To find the area of the microchip, we first need to find its length.
The diagonal of a square is related to the length of its sides as follows:
![d=l\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/m7r6zudguovr0ouyq3cjrcssnrj3agno8x.png)
where l = length of the side of the square
Therefore, this means that:
![l=\frac{d}{\sqrt[]{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/h4psrt53sm164lsiqytt2yakekczfs1ivx.png)
Therefore, the length of the side of the microchip is:
![\begin{gathered} l=\frac{0.141422}{\sqrt[]{2}} \\ l=0.1\operatorname{cm} \end{gathered}]()
The area of a square is given as:
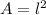
Therefore, the area of the microchip is:
![\begin{gathered} A=0.1^2 \\ A=0.01\operatorname{cm}^2 \end{gathered}]()
![\begin{gathered} A=0.1^2 \\ A=0.01\operatorname{cm}^2 \end{gathered}]()