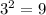Question

The similarity transformation (x, y) --> (1/3x, 1/3y) is performed on Square ABCD to create square A"B"C"D.

Answer 1

1. Since we're talking about a square, we'll have 4 sides that measure the same. This way, the perimeter is:

`\begin{gathered} 4s=4AB=4\cdot9 \\ \rightarrow36 \end{gathered}`

2. Notice that the transformation contracts distance by a factor of 3 (all distances are reduce to a third part).

Consequently, sides will be reduce to their third part too. This way, the new perimeter would be:

`\begin{gathered} 4\cdot((1)/(3)\cdot9) \\ \rightarrow12 \end{gathered}`

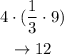
3. The area of the square is the lenght of its sides squared. This way, the area of ABCD is:

`9^2=81`

4. Knowing that the new sides measure 3, the new area would be:

`3^2=9`