We know that
• M is the midpoint of FR.
,
• F(-2,3) and M(3,0).
The midpoint formula is
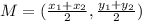
Where (x_1, y_1) represents point F and (x_2, y_2) represents point R (the missing point). So, our job is to find (x_2, y_2). Let's replace the information we have so far
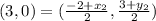
Let's separate the coordinates, that is, the horizontal coordinate 3 belongs to the horizontal coordinate on the other side of the equation, and the vertical coordinate 0 belongs to the vertical coordinate on the other side of the equation. So, we can rewrite the equation we have as two equations.

The first equation will give us the horizontal coordinate of point R, and the second equation will give us the vertical coordinate of point R. Let's solve both of them
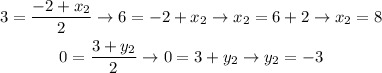
Therefore, the missing endpoint is (8,-3).
The image below shows all three points.