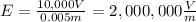Question

4:01HOMEWORKThe parallel plates of a vacuum capacitor are 5mm apart and have 2m ^ 2 in area. A potential difference of 10,000 V (10.0 kV) is applied across the capacitor. Calculate a) the capacitance, b) the charge on each plate, and c) the magnitude of the electric field in the space between them.

Answer 1

RESPUESTA

a) C = 3.54 x 10⁻⁹ F = 3.54 nF

b) Q = 35.4 x 10⁻⁶ C = 35.4 μC

c) E = 2,000,000 V/m

EXPLICACIÓN

a) La capacitancia de un capacitor de placas paralelas se define como la razón entre la magnitud de la cantidad de carga en cada placa y la diferencia de potencial aplicado. A su vez, ésta depende de la geometría del capacitor. La ecuación que la define es:

`C=\epsilon_0\cdot(A)/(d)`

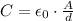
donde C es la capacitancia, A es el área de las placas y d es la distancia que separa las placas. Además ε0 es la permitividad del vacío. En general la fórmula también incluye la permitividad relativa del material dielétrico (el material entre las placas del capacitor) pero en este problema no nos interesa, dado que el material entre las placas de este capacitor es el vacío.

De esta manera, si reemplazamos los datos de este problema:

• ε0 = 8.85 x 10⁻¹² F/m

,

• A = 2 m²

,

• d = 5 mm

Nota que tanto la permitividad como el área de las placas tienen unidades de metros, pero la distancia de separación entre placas está en milímetros, por lo tanto debemos convertirla a metros:

Ahora sí, reemplazamos en la ecuación de arriba y obtenemos la capacitancia:

`C=8.85\cdot10^(-12)(F)/(m)\cdot(2m^2)/(0.005m)=3.54\cdot10^(-9)F`

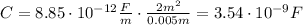
Cuando escribimos una cantidad en notación científica, y el exponente del 10 es -9 podemos no escribir esta parte y usar el prefijo nano. De esta manera, decimos que la capacitancia es de 3.54 nF.

b) La carga de las placas podemos obtenerla de la otra ecuación para definir la capacitancia:

`C=(Q)/(V)`

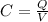
C es la capacitancia que encontramos en el punto a), V es la diferencia de potencial aplicada y Q lo que estamos buscando, la carga de las placas. Del enunciado, tenemos que la diferencia de potencial es V = 10,000V. Reemplazando y resolviendo para Q:

`\begin{gathered} 3.54*10^(-9)F=(Q)/(10,000V) \\ Q=3.54*10^(-9)F\cdot10,000V \\ Q=3.54*10^(-5)C \end{gathered}`

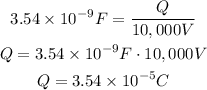
Si movemos el punto decimal un lugar hacia la derecha tenemos: 35.4 x 10⁻⁶ C, que puede llevar el prefijo de micro. Para el prefijo micro usamos la letra griega mu (μ). Entonces la carga de las placas es 35.4 μC

c) Finalmente, para encontrar la magnitud del campo eléctrico, utilizaremos la relación entre la diferencia de potencial y la distancia entre las placas:

`E=(V)/(d)`

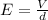
Reemplazando con V = 10,000V y d = 0.005m, el campo eléctrico es:

`E=(10,000V)/(0.005m)=2,000,000(V)/(m)`