Question

Montoya Construction needs to borrow $375,000 to build a road to install utilities in a small subdivision. It borrows the funds at 8% for 90 days. When interest rates were high in 1980, the interest rate would have been 20%. Find the difference in interest between the two rates.

Answer 1

Step 1

Given;

`\begin{gathered} \text{Principal(p)= \$375000} \\ \text{First rate = 8\%=}(8)/(100)=0.08 \\ \text{Second rate = 20\%= }(20)/(100)=0.2 \\ \text{Time}=(90)/(365)=(18)/(73) \end{gathered}`

Required; To find the difference in interest between the two periods.

Step 2

State the formula for simple interest

`A=P(1+rt)`

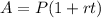
Step 3

Find the interest when the rate is 8%

`\begin{gathered} A=375000(1+(0.08*(18)/(73)) \\ A=375000(1+(36)/(1825)) \\ A=\text{\$}382397.26 \end{gathered}`

Therefore the interest is given as;

`A-P=382397.26-375000=\text{\$}7397.26`

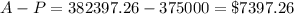
Step 4

Find the interest in 1980 with a 20% rate

`\begin{gathered} A=375000(1+(0.2*(18)/(73)) \\ A=\text{\$}393493.15 \end{gathered}`

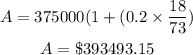
The interest is given as;

`A-p=393493.15-375000=\text{\$}18493.15\text{ }`

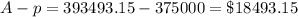
Step 5

Find the difference in interest between the two rates.

`\text{\$}18493.15-\text{\$}7397.26=\text{\$}11095.89`

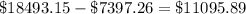
Hence, the difference in interest between the two rates = $11095.89