Question

Part IOnce you have constructed the parabola, use GeoGebra to display its equation. In the space below, rearrange the equation of the parabola shown in GeoGebra, and check whether it matches the equation in the vertex form that you wrote in part G. Show your work.Equation: y^2 + 16x - 4y = -20Equation of part G: x = 1/16 (y - 2)^2 + (-1)

Answer 1

Equivalent equation: x = -1/16 (y - 2)² + (-1)

Which is not equal to x = 1/16 (y - 2)² + (-1)

Step-by-step explanation:

The given equation is

y² + 16x - 4y = -20

To know if is equivalent to x = 1/16 (y - 2)² + (-1), we need to have the x on one side and the y on the other, so subtract 16x from both sides

y² + 16x - 4y - 16x = -20 - 16x

y² - 4y = -16x - 20

Then, we need to complete the square on the left side. So, we need to add (b/2)² on both sides, where b is the number besides y.

(b/2)² = (-4/2)² = (-2)² = 4

By adding 4 to both sides, we get

y² - 4y + 4 = -16x - 20 + 4

(y - 2)² = -16x - 16

Factorize -16 from the right side

(y - 2)² = -16(x + 1)

Divide both sides by (-16)

`\begin{gathered} (1)/(-16)(y-2)^2=(-16(x+1))/(-16) \\ \\ -(1)/(16)(y-2)^2=x+1 \end{gathered}`

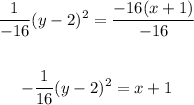
Finally, subtract 1 from both sides

`\begin{gathered} -(1)/(16)(y-2)^2-1=x+1-1 \\ \\ -(1)/(16)(y-2)^2+(-1)=x \end{gathered}`

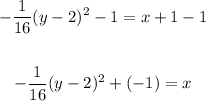
Therefore, the equation is

x = -1/16 (y - 2)² + (-1)

We can see that it doesn't match the equation x = 1/16 (y - 2)^2 + (-1) because the sign of 1/16