Question

Determine if triangle HIJ and triangle KLM are or are not similar

Answer 1

The two triangles are said to be similar if they satisfy these conditions(SAS):

1. The two sides of a triangle are in the same proportion as the two sides of another triangle.

2. The angle inscribed by the two sides in both the triangle is equal.

Given

Triangle HLJ has the following properties:

Sides: 22, 19

Inscribed angle = 66 degrees

Triangle KLM has the following properties:

Sides: 66, 57

Inscribed angle = 66 degrees

Solution

We can see that:

`\begin{gathered} (IJ)/(LM)\text{ = }(IH)/(LK) \\ (22)/(66)\text{ = }(19)/(57) \\ \text{Inscribed angle = 66}^0\text{ for both triangles} \end{gathered}`

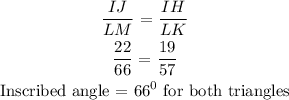
Hence:

`\Delta\text{ HIJ }\approx\text{ }\Delta KLM`

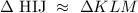
Answer: we can conclude that the triangles are similar