Question

a rectangle is drawn so the width is 16 inches longer than the height. if the rectangles diagonal measurment is 80 inches find the height round to one decimal place_____inches

Answer 1

the height is 48 inches

Step-by-step explanation

Step 1

we have a rigth triangle, so , we can use Pythaogras theorem to find the length of the legs

Let

hypotenuse=80 in

leg1=height

leg2=wide=16+height

using the theorem

`\begin{gathered} \text{leg}1^2+leg2^2=hypotenuse^2 \\ \text{replacing} \\ \text{height}^2+(16+height)^2=80^2 \\ \text{Let height=h} \\ h^2+(16+h)^2=80^2\text{ Equation (1)} \end{gathered}`

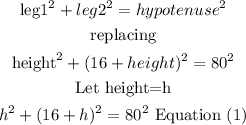
Step 2

solve for h

`\begin{gathered} h^2+(16+h)^2=80^2\text{ Equation (1)} \\ h^2+16^2+2\cdot16\cdot h+h^2=80^2\text{ Equation (1)} \\ h^2+256+32h+h^2=6400 \\ 2h^2+32h+256-6400=0 \\ 2h^2+32h-6144=0 \\ u\sin g\text{ the quadratic formula} \\ h=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ a=2,\text{ b=32, c=-6144} \\ \text{replacing} \\ h=\frac{-32\pm\sqrt[]{-32^2-4\cdot2\cdot-6144}}{2\cdot2} \\ h=\frac{-32\pm\sqrt[]{50176}}{4} \\ h=(-32\pm224)/(4) \\ we\text{ can take just the positive value( because we are looking for a distance)} \\ h=(-32+224)/(4) \\ h=(192)/(4) \\ h=48 \end{gathered}`

so, the height is 48 inches