Solution
The question tells us the area of a rectangular prism is 350cm² and its square base has an area of 25cm². We are required to find the height of the prism.
Step-by-step explanation
- The formula for the total surface area of a rectangular prism is given by:
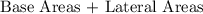
- A rectangular prism has 2 equal Base Areas and 4 equal Lateral Areas. This is illustrated below:
- This implies that the Base Areas is gotten by:
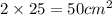
Thus, we can find the Lateral Areas as follows:
![\begin{gathered} \text{ Total Surface Area (TSA)}=\text{ Base Areas }+\text{ Lateral Areas} \\ 350=50+\text{Lateral Areas} \\ \text{Subtract 50 from both sides} \\ \text{ Lateral Areas }=350-50=300 \\ \\ \text{But we know that there are 4 equal Lateral Areas. Thus, we can find the area for just one lateral face as follows:} \\ \text{Let the area of one lateral face be L} \\ 4L=300 \\ \text{Divide both sides by 4} \\ (4L)/(4)=(300)/(4) \\ \\ \therefore L=75 \end{gathered}]()
- This means that just one lateral surface has an area of 75 cm²
- If one of the lateral face is made up of the base length and the height of the rectangular prism. We are looking for this height, thus, we need to know the base length of the prism.
- Luckily, we know that the Base is a square. Thus, we can easily find the length of the base as follows:
![\begin{gathered} \text{Let the length of the Base be }l \\ l* l=25 \\ l^2=25 \\ \text{Take the square root of both sides} \\ l=\sqrt[]{5} \\ l=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/15zm2vnym5m8wox1l016wy9el7vz5ulplo.png)
- Now that we have the length of the base, we can proceed to find the height of the prism as follows:

Final Answer
The height of the prism is 15 cm.