Question

while walking in the country, you count 30 heads and 82 feet in a field of pigs and chickens. how many of each animals are there

Answer 1

Let 'p' and 'c' denote the number of pigs and the number of chickens, respectively.

Given that there are 30 heads, and we know that each animal has a single head,

`\begin{gathered} p+q=30 \\ q=30-p \end{gathered}`

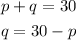
Knowing that a pig has 4 legs, and a chicken has 2 legs. It is given that the total number of legs is 82,

`\begin{gathered} 4p+2q=82 \\ 2p+q=41 \end{gathered}`

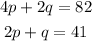
Substitute the value of 'q' from first equation into the second equation,

`\begin{gathered} 2p+(30-p)=41 \\ 2p-p=41-30 \\ p=11 \end{gathered}`

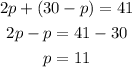
Substitute the value in the first equation,

`\begin{gathered} q=30-11 \\ q=19 \end{gathered}`

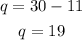
Thus, there are 11 pigs and 19 chickens.