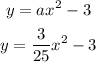Solution:
Given:
Based on the graph, it can be estimated that;
The vertex is at (0,-3) and the roots are at (-5,0) and (5,0)
Using the equation of a parabola in vertex form;
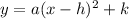
where;
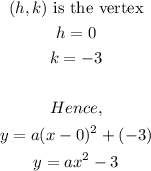
Using the point (5,0) to get the constant a;
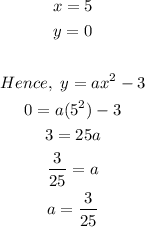
Hence, the equation of the parabola is;