Question

The table shows the results of rolling a die with unequal faces find each experimental probability as a fraction in simplest form.Rolling a 1 or 6?

Answer 1

We are asked to determine the probability of rolling a 1 or a 6. To do that we will use the following relationship:

`P(1\text{ or 6\rparen=}P(1)+P(6)`

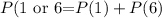
Therefore, we need to add the probability of getting a 1 and the probability of getting a 6.

The probability is the quotient of the number of occurrences divided by the sum of the total number of occurrences, like this:

`P(1)=(26)/(26+10+12+9+14+29)`

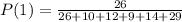
Solving the operations:

`P(1)=(26)/(100)=(13)/(50)`

Now, we determine the probability of getting a 6:

`P(6)=(29)/(26+10+12+9+14+29)=(29)/(100)`

Now, we add the probabilities:

`P(1\text{ or 6\rparen=}(13)/(50)+(29)/(100)=(11)/(20)`

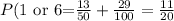
The probability is 11/20.