ANSWER :
The value of x is Option D.
![x=\frac{7\pm i\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/yjevgwibnhnetxektxap0y05yel7xd9d6f.png)
EXPLANATION :
From the given problem,
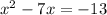
First step is to rewrite the equation in the form ax^2 + bx + c = 0
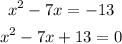
Second step is to use the quadratic formula in finding the values of x :
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
where a, b and c are the coefficients of the quadratic equation.
a = 1, b = -7 and c = 13
![\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4(1)(13)}}{2(1)} \\ x=\frac{7\pm\sqrt[]{49-52}}{2} \\ x=\frac{7\pm\sqrt[]{-3}}{2} \\ x=\frac{7\pm i\sqrt[]{3}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jwqdwwf7vgkkj9r6i4vi9y07q95pdd8cuw.png)
Note that i = √-1