Question

Solve for x by using the quadratic formula. If you have multiple solutions, list them separated by commas.4x2+12x=−12x

Answer 1

`\begin{gathered} \text{ Given} \\ 4x^2+12x=-12 \end{gathered}`

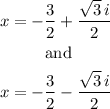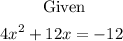
First, equate the given to zero, and determine its coefficients a,b, and c

`\begin{gathered} 4x^2+12x=-12 \\ 4x^2+12x+12=-12+12 \\ 4x^2+12x+12=0 \end{gathered}`

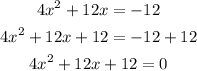
It is now in the standard form where a = 4, b = 12, and c = 12. Substitute these values to the quadratic formula and we get the following

`\begin{gathered} x = ( -b \pm √(b^2 - 4ac))/( 2a ) \\ x = ( -12 \pm √(12^2 - 4(4)(12)))/( 2(4) ) \\ x = ( -12 \pm √(144 - 192))/( 8 ) \\ x = ( -12 \pm √(-48))/( 8 ) \\ x = ( -12 \pm 4√(3)\, i)/( 8 ) \\ \; \\ x_1=( -12 )/( 8 )+(4√(3)\, i)/( 8 ) \\ x_1=-( 3)/( 2 )\pm( √(3)\, i)/( 2 ) \\ \; \\ x_2=( -12 )/( 8 )-(4√(3)\, i)/( 8 ) \\ x_2=-( 3)/( 2 )-( √(3)\, i)/( 2 ) \end{gathered}`

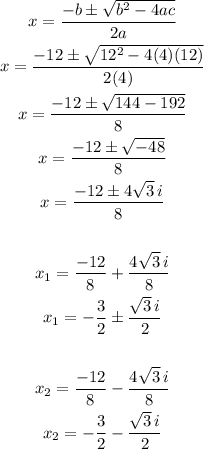
Therefore, the solution to the equation is

`\begin{gathered} x=-( 3)/( 2 )+( √(3)\, i)/( 2 ) \\ \text{ and} \\ x=-( 3)/( 2 )-( √(3)\, i)/( 2 ) \end{gathered}`