We are given the right angle triangle.
First, let us find the length of side BC using the Pythagorean theorem.
![\begin{gathered} AC^2+BC^2=AB^2 \\ 12^2+BC^2=15^2 \\ BC^2=15^2-12^2 \\ BC^2=225-114 \\ BC^2=81 \\ BC=\sqrt[]{81} \\ BC=9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yydvzf5b50mtzomn1vv950i8wsibonecex.png)
Therefore, the length of side BC = 9
The angle m∠C is clearly 90°
Let us find the angle m∠A and m∠B
We can use the law of sines to find the m∠A and m∠B
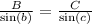
Let us substitute the values and find m∠B
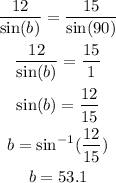
So the angle m∠B is 53.1°
Now we have two angles so the third angle can be found by
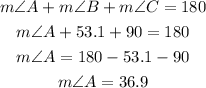
Therefore, the angles are
BC = 9
m∠A = 36.9°
m∠B = 53.1°
m∠C = 90°
Therefore, the correct option is A