Ok, in the pic we can see that tha quadrilateral is an isosceles trapezoid, so we know that:
The angles of the bases must have the same measure two by two and the angles adjacent to the opposite bases are supplementary. So, ising this, we get:
The measure of W= measure of X=112° and this mean also that angles Y and Z are equal.
So we have:
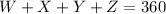

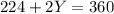
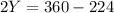
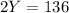
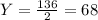
The measure of angles Y and Z are 68° each one of them.