Question

A)graph the function: F(x)= 2 ^-(x+1) -3B)domain of the function?C)range of the function?D) equation of the asymptote?E)y-intercept of the graph?

Answer 1

The given function is:

`f(x)=2^(-(x+1))-3`

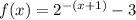
A) The graph of the function f(x) is plotted below

B) The domain of the function f(x) is a set of the values of x that makes the function valid

The domain of f(x) is a set of all real numbers

Domain: (-∞, ∞)

C) To find the range of the function, substitute x = ∞ into f(x) to get the point where f(x) is invalid

`\begin{gathered} f(\infty)=2^(-(\infty+1))-3 \\ f(\infty)=0-3 \\ f(\infty)=-3 \end{gathered}`

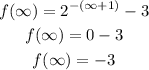
Therefore, the range function is written as:

Range: f(x) > -3 or (-3, ∞)

D) Equation of the asymptote

For an exponential function of the form f(x) = a(b^x) + c, the horizontal asymptote is usually y = c

Therefore, the horizontal asymptote of the given function is y = -3

The function f(x) does not have a vertical asymptote

E) y-intercept of the graph

Substitute x = 0 into f(x)

`\begin{gathered} f(0)=2^(-(0+1))-3 \\ f(0)=2^(-1)-3 \\ f(0)=(1)/(2)-3_{} \\ f(0)=-(5)/(2) \end{gathered}`

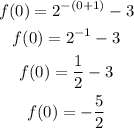
The y-intercept = (0, -5/2)

o