Question

A college student realized that he was spending too much money on music. For the remaining 5 months of the year his goal is to spend amean of $50 a month towards music. How much can he spend in December, taking into consideration that in the other 4 months hespent $35, $40, $100, and $30, respectively? Round your answer to two decimal places, if necessary.

Answer 1

The formula to find the mean of a data set is:

`\text{ Mean }=\frac{\text{ Sum of data points}}{\text{ Number of data points}}`

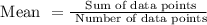
Now, let x be the amount of money he can spend in December. Then, we have:

`\begin{gathered} \text{ Mean }=\text{\$}50 \\ \text{\$}50=\frac{\text{\$}35+\text{\$}40+\text{\$}100+\text{\$}30+x\Rightarrow\text{ Money spent in each month}}{5\Rightarrow\text{ Number of months}} \end{gathered}`

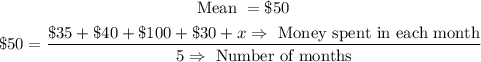
Then, we can solve the above equation for x:

`\begin{gathered} \text{\$}50=\frac{\text{\$}35+\text{\$}40+\text{\$}100+\text{\$}30+x}{5} \\ \text{ Add similar terms in the right side of the equation} \\ \text{\$}50=\frac{\text{\$}205+x}{5} \\ \text{ Multiply by 5 from both sides of the equation} \\ \text{\$}50\cdot5=\frac{\text{\$}205+x}{5}\cdot5 \\ \text{\$}250=\text{\$}205+x \\ \text{ Subtract \$205 from both sides of the equation} \\ \text{\$}250-\text{\$}205=\text{\$}205+x-\text{\$}205 \\ \text{\$}45=x \end{gathered}`

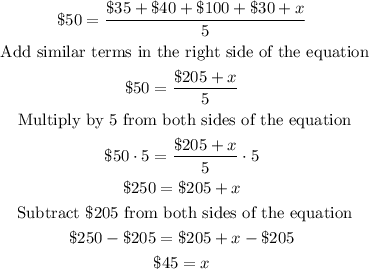
Therefore, he can spend $45 in December to meet his goal of spending a mean of $50 per month for the remaining 5 month of the year.