We have two right triangles, in order to find the missing sides we will use the Pythagorean Theorem
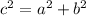
For the little one we have
c=20
a=16
b=x
we substitute the values
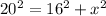
we isolate the x
![x=\sqrt[]{20^2-16^2}](https://img.qammunity.org/2023/formulas/mathematics/college/hsebzzr0bafxjsvp9aorr9msht3y8tlo0n.png)
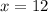
Then for the bigger triangle
c=y
a=18
b=12
we substitute the variables
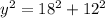
we isolate the y
![y=\sqrt[]{18^2+12^2}](https://img.qammunity.org/2023/formulas/mathematics/college/o1zmwnxdk6067cfbje0zs1372vr7osoh9p.png)
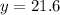
As we can see the correct choice is A. x=12 and y=21.6