Question

Hi, teacher I was absent these days and I didn’t understand anything about this lesson and I need help this is not count as a test it’s just hw please help thanks a lot

Answer 1

For this problem, we are given a certain trigonometric expression shown below:

`\frac{2\tan((2\pi)/(3))_{}}{1-\tan^2((2\pi)/(3))}`

And we need to represent it as a sin, tan, or cos of a double angle. The first thing we can do to make this easier is to assign a variable to 2pi/3, which we can see below:

`x=(2\pi)/(3)`

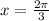
Now we can replace the expression above with the original one:

`\frac{2\tan(x)_{}}{1-\tan^2(x)}`

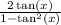
We know that a tangent is a division between a sine and a cosine. We can replace the tangent on the expression above with that division:

`\frac{2(\sin(x))/(\cos(x))_{}}{1-(\sin^2(x))/(\cos^2(x))}`

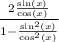
Now we need to find the LCM on the denominator, so we can transform the denominator into a single fraction.

`\frac{2(\sin(x))/(\cos(x))_{}}{(\cos^2(x)-\sin^2(x))/(\cos^2(x))}`

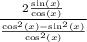
Now, we have a division between two fractions. We need to conserve the first fraction and multiply it by the inverse of the second one.

`\begin{gathered} 2(\sin(x))/(\cos(x))\cdot(\cos^2(x))/(\cos^2(x)-\sin^2(x)) \\ \frac{2\sin(x)\cos^{}(x)}{\cos^2(x)-\sin^2(x)} \end{gathered}`

We have a trigonometric identity that says the following:

`2\sin (x)\cos (x)=\sin (2x)`

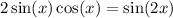
And another that states this:

`\cos ^2(x)-\sin ^2(x)=\cos (2x)`

If we replace the two identities above on our fraction, we will obtain:

`\frac{2\sin(x)\cos^{}(x)}{\cos^2(x)-\sin^2(x)}=(\sin(2x))/(\cos(2x))`

The division between the sine and cosine is equal to the tangent, therefore we have:

`(\sin(2x))/(\cos(2x))=\tan (2x)`

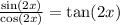
We know the value for x, therefore we can replace it on the expression above and find the value for the tangent.

`\begin{gathered} \tan (2\cdot(2\pi)/(3)_{}) \\ \tan ((4\pi)/(3)_{}) \end{gathered}`

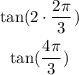
This concludes that:

`\frac{2\tan((2\pi)/(3))_{}}{1-\tan^2((2\pi)/(3))}=\tan ((4\pi)/(3)_{})`

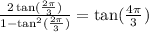
The correct option is B, and the value we need to input on the blank box is 4pi/3.